The use of anomalies in calculating temperature data allows NOAA/NASA to shift the baseline years undetected.
The graph below shows how NCDC tampers with the US temperature record, to create a non-existent warming trend.
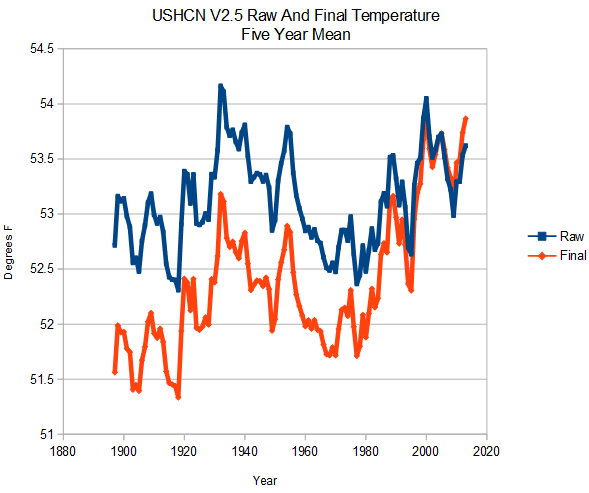
Here is NCDC’s 1991 version of US temperatures in absolute temperatures.
www1.ncdc.noaa.gov/pub/data/cmb/bams-sotc/climate-assessment-1981-1990.pdf
The next graph shows the NCDC 1991 version and 2014 version in absolute temperatures. They have cooled the past. This has nothing to do with station loss. It is about altering the data.
Now look what happens if I use temperature anomalies, as some people on both sides of the debate demand. As long as they cool all of the years during a baseline period (in this example 1951-1980 – the one used by NASA) by an approximately equal amount, most of the data tampering during that period is hidden.
The trick NCDC pulls is to stop cooling temperatures after the end of the baseline period. This allows them to create a huge fake warming in recent years, which is largely hidden using anomalies.
By using the anomaly method, the data tampering becomes invisible. Is it the goal to hide the tampering, or do they just not understand what they are doing?
Additionally, it is utterly absurd to believe that station loss since 1990 has selectively targeted warmer stations, and particularly doing so increasingly over time. That is statistically impossible.




From my perspective this is a pretty good argument. Part of science is scientific method, and all that, but a big part of science is being able to compare results, and rapidly identify inconsistencies.
That said, can WUWT be persuaded to also abandon anomalies?
If I as technically competent engineer provide test data manipulated in this way to the US Government to prove that a system I designed for them was performing as I said it was… I would currently be serving a well deserved sentence in a Federal Prison for criminal fraud… because it IS fraud (and I don’t donate to the Democrat party.) There is no way on God’s (or Gaia’s) green earth that this was in any way, shape, matter or form a “mistake” in processing data to deal with “anomalies.” That’s an awfully convenient set of anomalies that changes a trend from negative to positive… Hmmmmm.
Once again I ask, if there were warming, why does any last frost date continue moving later and later in OK?
Great point! I wish we’d been publicizing raw data and actual temperature numbers all these years, so that the public might notice and ask more questions about why the average temperature of 1927 is now different than it was a few years ago.
I’m not sure you quite understand what we are talking about when we suggest using anomalies. We aren’t asking you to rebaseline series after averaging all the absolute temperatures, rather we are asking you to change the individual station data into anomalies.
Anomalies won’t provide an estimate of absolute temperatures for the U.S. at a given year, at least by themselves. Averaging absolutes won’t either, since they do a poor job of sampling the underlying heterogenous climatological field (due to elevation and other factors). Anomalies will provide an unbiased estimator of the rate of temperature change over time, which is what most of us are concerned with. Averaging absolutes will not provide an unbiased estimator of rate of change over time if the composition of the station network has changed, which has happened in the case of USHCN.
Also, you seem to be conflating the impacts of TOBs corrections, homogenization, and infilling. Anomalies effectively remove bias due to changing network station composition over time (e.g. the bias you are incorrectly attributing to infilling); they don’t magically “hide” adjustment done to correct for changes in time of observation, station moves, instrument changes, UHI, etc.
If there has been selective loss of rural stations, then using anomalies, gridding and infilling data will hide it, and produce a spurious multiplied warming trend.
Why would you want to do that Zeke?
I have demonstrated repeatedly through experiment that random dropout of 30% of data has little effect on the absolute temperature. The divergence between raw and adjusted absolute temps indicate that the data loss is not random, and the adjustments are skewing the data.
Do you normally refer to yourself as plural?
If your assertions are correct then reduce the number of stations to one representative station for all of the US, and do all adjustments and infilling from that station’s data.
That still satisfies your logic?
If not when are there too few stations? And how can you ever know?
So why not from now on, also publish the “average temperatures” for each year you create an “anomaly” for? Then, as time goes on, even simpletons like me can see there is nothing to what Steve has to say. It’s “data” that already exists, it has to in order to calculate the “anomaly”, so just…. publish it. Simple. Problem solved. So I expect the next product update, will also include the “average temperature” used to calculate the “anomaly”. Put this question to rest, and just publish the “data”.
You do know the “average temperature” for every year that you create an “anomaly” for….. don’t you? Do you?
Zeke,
“Averaging absolutes won’t either, since they do a poor job of sampling the underlying heterogenous climatological field (due to elevation and other factors).”
I know you keep asserting this, and this might even be true. But can you demonstrate it? One would expect some effect on temperature trends due to a change in composition, but why wouldn’t it largely be random overall, with most of the effect on trend therefore cancelling itself out? (Because station locations are intentionally widely distributed across the US. The design was intended to avoid this eventuality as much as possible.)
I’m happy to accept your claim, but you need to demonstrate it, not simply assert it. Have you done this somewhere? Otherwise you’re asking people to accept the claim that if you loose stations, the result is *always* more warming. Why would anyone simply believe such an unusual assertion? Now, I accept it might be true, but I don’t understand why you think anyone should believe this remarkable coincidence just because you say so?
A demonstration would indeed be helpful. I can see how using an anomaly would give one a better idea of what temperatures are doing if you have station dropout but it’s not clear to me at all how random station dropout would result in a trend one way or another unless the stations dropping out were much lower or much higher than the average.
Zeke- for the good of your argument you need to come back here. A lot of us are waiting.