I started writing about climate nine years ago with this article in The Register. I pointed out that Arctic experts are wildly incompetent hacks, and came under attack by Walt Meier at NSIDC for doing so.
Arctic ice refuses to melt as ordered • The Register
Here are the expert predictions I was making fun of – Arctic to be ice-free in 2008.
Expert: Arctic polar cap may disappear this summer_English_Xinhua
North Pole to be ice-free in 2008.
North Pole May Be Ice-Free for First Time This Summer
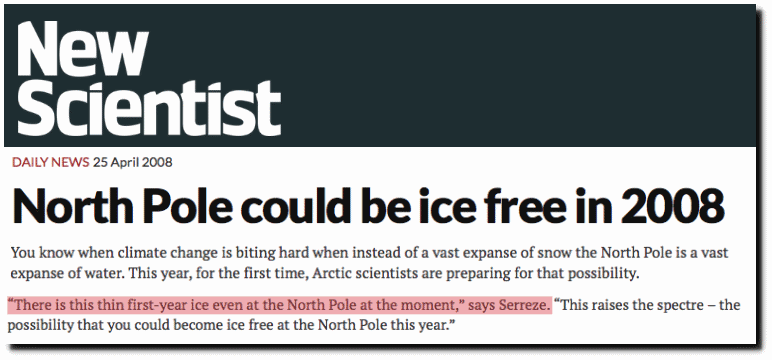
North Pole could be ice free in 2008 | New Scientist
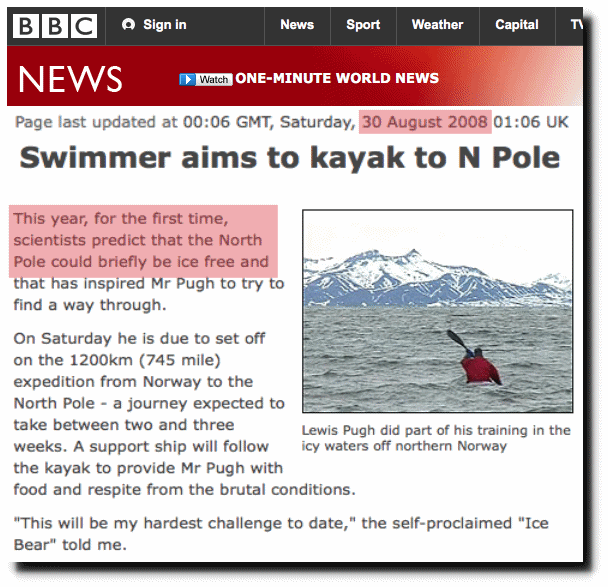
Based on the advice of these experts, Lewis Pugh tried to kayak to the North Pole.
BBC NEWS | UK | Swimmer aims to kayak to N Pole
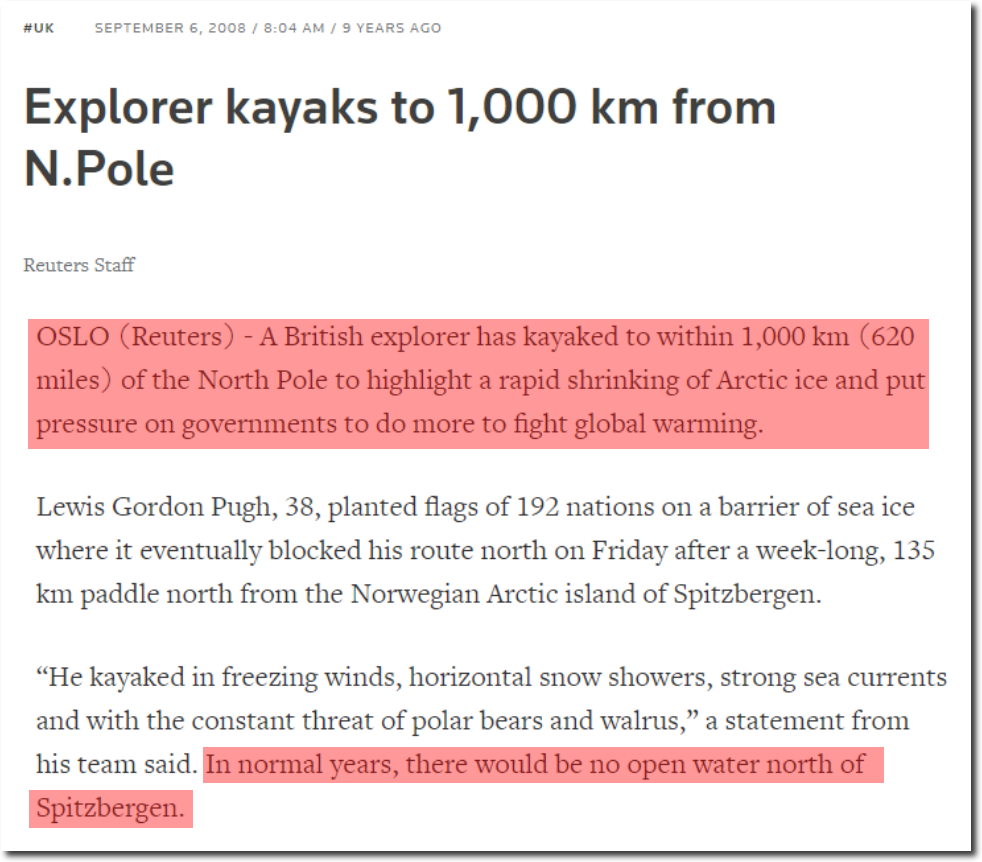
Pugh didn’t get very far, and the fake news press quite predictably declared victory in defeat.
Explorer kayaks to 1,000 km from N.Pole
The Reuters story read :
In normal years, there would be no open water north of Spitzbergen.
As with almost everything else reported by the press, this was fake news which the author simply made up. Here is some actual news from 95 years ago.
last winter, the ocean did not freeze over even on the north coast of Spitzbergen.
US Consul Norway, 1922
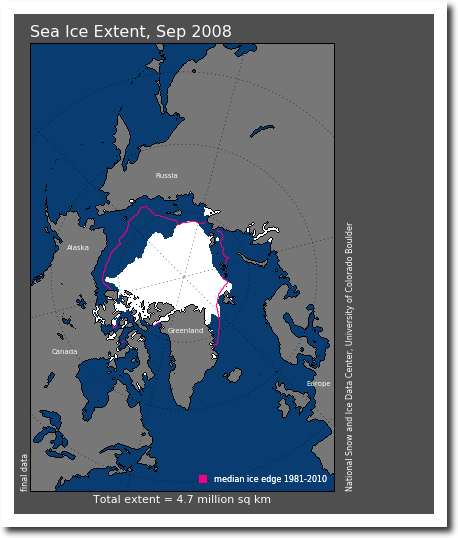
Arctic ice didn’t disappear in 2008, and there was more ice near Spitzbergen than normal.
N_200809_extn_v2.1.png (420×500)
The leading experts from Norway, Canada and the US had no clue what they were talking about, and the press lied and never retracted their fake stories – but nothing unusual about that.
Science is the belief in the ignorance of the experts
– Richard Feynman
That isn’t the prediction I am making fun of in this post however. Ten years ago, America’s top experts predicted the Arctic would be ice-free by 2012. They said “The Arctic is screaming.”
Star-News – Google News Archive Search
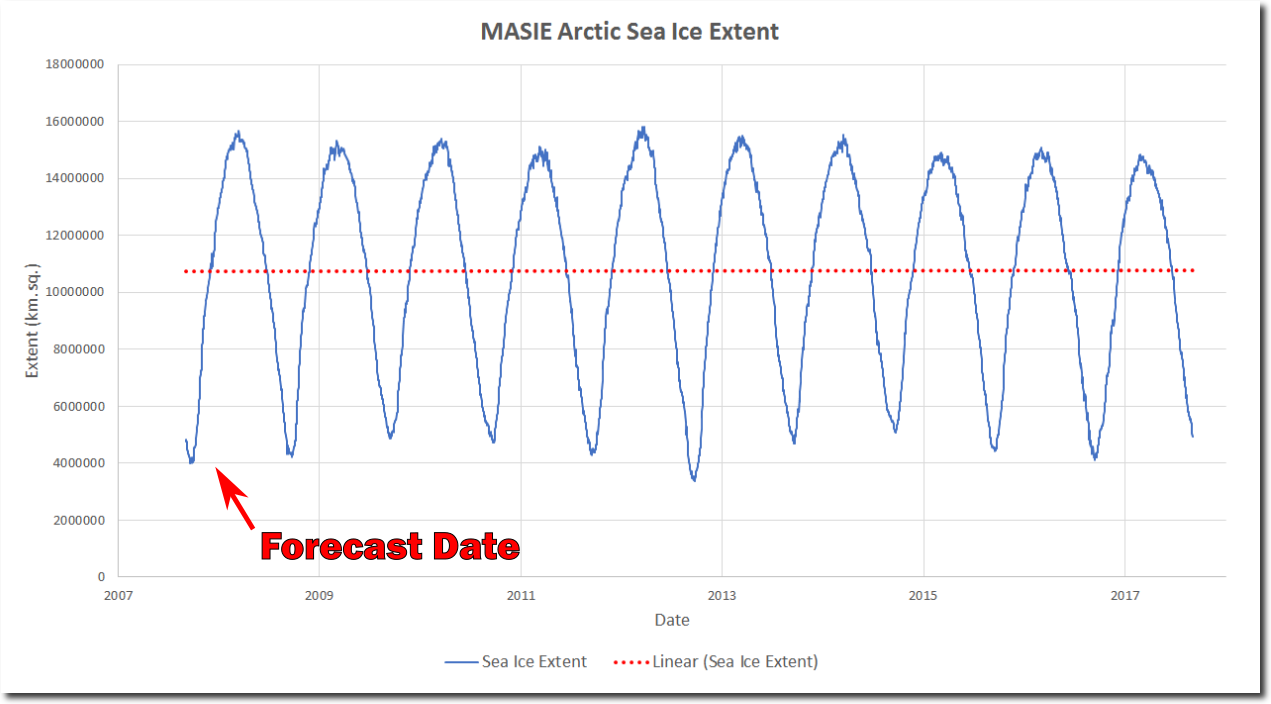
Their forecast was based on the commonly held superstition that 0.0004 mole fraction atmospheric CO2 controls ice behavior, and the forecast of course failed – because they had no clue what they were talking about. There has been no change in Arctic sea ice extent since those forecasts were made a decade ago..
masie_4km_allyears_extent_sqkm.csv
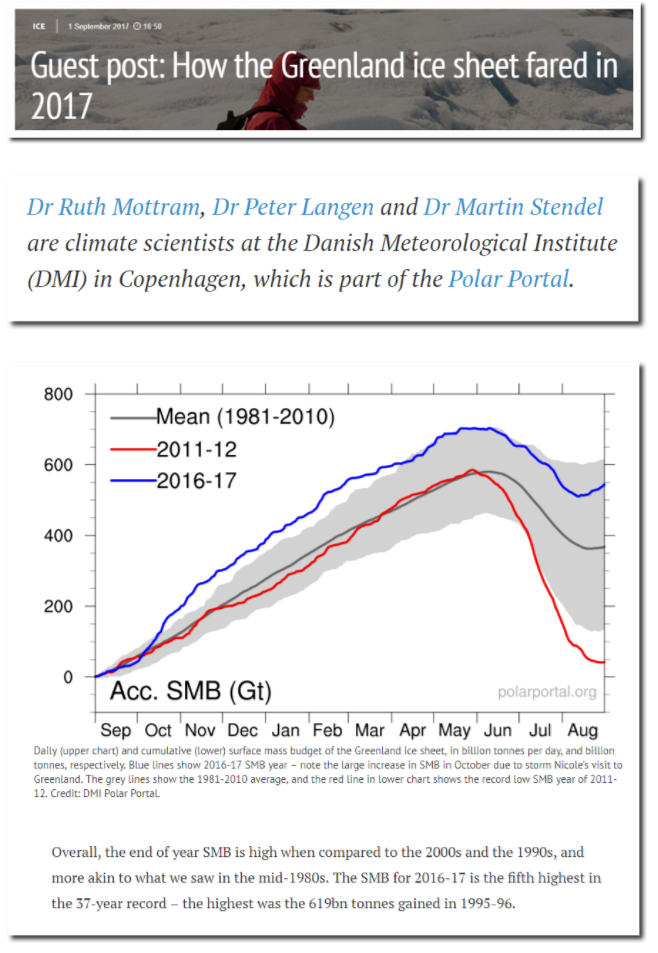
The 2007 article said Greenland was melting down and was the canary in the coal mine. Ten years later Greenland had their fifth largest mass gain on record.
Guest post: How the Greenland ice sheet fared in 2017 | Carbon Brief
In that 2007 article, scientists announced that a weakened jet stream caused drought in the Southeast.
This week they claimed the exact opposite, saying a weakened jet stream causes floods.
CO2 is changing the jet stream in ways that will create more Harveys – ThinkProgress
Climate scientists have no clue what they are talking about. Global warming theory is junk science, and there appear to be no limitations on how these crooked snake oil salesmen will change their story to keep the scam alive.
Where’s Canute when you need him?
Another direct hit on the Grifftard by Tony …. Griffiepoo is listing badly and taking on water … headed to Davy Jones locker any moment!!
It’s worse than you thought, eh Griffy?
Griff is a troll that spams the Global Warming Alarmist Propaganda on most Skeptic blogs.
When theory trumps reality humans devolve.
That’s a really impressive track record of failures
by people who still think they are absolutely right.
Reminds me of Monty Python & the holy grail,
when the black knight loses both arms and legs during the fight and then says “All right!We’ll call it a draw.”(he obviously became a climate scientist after fight)
Wonder we(a)ther the kayak guy tried his trip to the north pole again :)
As AMO peaked and heads to its low, Arctic ice has to grow.
I noticed that Michael Mann and other “climate scientists” are not out there right now in real time telling us how “climate change” is causing Irma to track towards us or how it helped in it’s formation or strengthening. They don’t have the balls to do actual real time forecasts that could be evaluated for their accuracy in a matter of a week or so but they sure can tell you what the weather will be 10, 30, 50, 100 years from now!
If you can’t hit the broad side of a barn at 25 feet, you aren’t going to hit the target at 100 meters.
Of course you can hit a target at a 100 meters after you’ve missed at 25 feet. It’s called pure, dumb luck.
I think humans in the future will look back at this current global warming farce/hysteria and view it the same way we do the European witch hunts during the 16th to 18th centuries.
Zealots will always be crazy and keep doubling down on their beliefs hence why they’re zealots.
Oh and I have to once again say thanks for finding those old newspaper articles that show how nutty and fraudulent these people are.
It’s particularly telling that they seem happy that the hurricane drought is over, that SE Texas was ravished. They even seem to hope that Irma will hit and cause even more pain and destruction.
Well, they haven’t had a lot of pleasure or joy from hurricanes in the last 11 or so years.
I hope some of then are hit really hard by the next one, so they can be happy.
Yes, David barber said the ice was “rotten”. Hmmmmm, it takes a long time to rot to nothing.
Later, I will post the interview in the Winnipeg Free Press where the guy said Hudson Bay would be ice free in the WINTER in 5-10 years.
We have to keep track of that one for Griffy & co.
and yet the trend in extent, volume, thick MYI ice, ice thickness continues to be down.
The ice now stays thin/at a lower extent than historically through the winter too.
Stop hallucinating, Ms Griff, and dry your bed sheets. What history are you prattling about?
I believe we have discovered why alarmists are reporting a rise in localized humidity levels.
Climate scientists at the University of East Anglia must refocus their research on catastrophic localized humidity rise in London suburbs.
Depends.
How long before we see a peer-reviewed paper with graphs showing
causationdependence?Maybe we will see Ms Griff make the cover, once their submission is thoroughly peereviewed…
Earlier this week Tony showed how stupid your MYI statement is but you continue to repeat the nonsense. You are a little prick and I hope u freeze in the dark this winter!
Fat chance. Ms Griff only denies life sustaining resources to others.
A very recent trend that is better than the alternative. And who died as a result Ms Griff? Time to stop your lying and your genocide.
I suppose everybody is hoping there is good Arctic sea ice accumulation this winter. In that event, we are off to a good start. All eight Maritime buoys above 80N I can pull up on the NWS site are reporting temps no higher than 29F as of 1500 UTC today. Buoy 48278 at 82.5N is reporting 13F, after a low overnight of -1F. Great news, right?
It depends. The cold will increase the heating bills of the natives but it won’t stop climate cultists from hallucinating they are getting fried.
Griff-
there is a reason why the massive sea level rise of the past thousands of years(which for sure did not happen because of co2 or AGW or whatever the name of your satan is)) has dropped to todays lows.
It is the fact that overall ice has almost stopped melting.
The less ice melts ,the lower the sea level will rise.
Of course arctic ice is of no relevance but greenland ice is and antarctic
land ice.
If there is a massive loss on ice there is NO way to hide the resulting sea level rise.
And if you want to know how much sea level is rising,
just compare photos of buildings from a hundred years ago((you need several from every different era to balance tide-effects )) and compare it with todays photos
or just as old people.
As you live on an island you should have no problems to find out wether
there have been massive losses by flooding or not.
Maybe you’ll find out that the last apocalyptic 30 years has been as boring as the 30 years before and the 30 years before those etc.
BTW-with a little less arrogance you may even realise one day how amazing it is that such complicated and huge systems as our climate or our atmosphere and the sun can run on such a constant level without many changes – then you’ll be able to realise that such huge system cannot be brought down by a shitty meaningless little bit of co2.
That’s for sure.
PS-
the only reason you do not believe in global cooling is that your masters
stopped pushing the global cooling crap some decades ago.
But i’m pretty sure your parents did and forgot about it.
((have you ever heard that scientist did a complete 180 in science?
No!The reason is simple-you can not miss your target so much when doing research.
Now such thing may happen from time to time-but usually you need a revolutionary breakthrough+ this breakthrough does not abrogate
the previous teaching but add new standards which become part of the overall teaching.
The reason is simple why climate science could do such an amazing 180,
why global cooling all of a sudden turned into global warming,
why they all of a sudden “discovered” satellite data showing hiatus
are not usefull,
why they all of a sudden “discovered” that oceans absorbed so much energy
because climate science is no science.
(maybe it was a long time ago,but no more)
Just a bunch of gurus struggling to keep their religion and god alive using all strategies religions do use to keep their sheep in line.
satan= co2
hellfire= global warming
unbelievers= deniers
allah=climate
prophets=climate scientists((with the huge difference that prophets and fortune tellers are at least sometimes right with their predictions)
MYI increasing according the Russians.
Both NSIDC and MASIE have 2017 extent GREATER THAN 2007, 2008, 2011, 2012, 2015, and 2016
FACTS is facts, little bed-wetter.
STOP LYING..
It is noted you still haven’t answered the simple question..
What SHOULD the current level of Arctic sea ice be?
Take into account the fact that levels through the first 7000+ years of the Holocene were often summer ice free. !
So not only are you being BLATANTLY DISHONEST, you are actually a CLIMATE CHANGE DENIER and a chicken-little COWARD.
“at a lower extent than historically through the winter too.”
yet another BLATANT LIE. all you have is refusal to recognise science
SCIENCE tells us that current levels are above those of 90-95% of the last 10,000 years
Why do you continue to DENY SCIENCE. !!
You are a CLIMATE CHANGE DENIER, as well as a perennial bed-wetter.
You are still full of it Griff. Show us the 10 year minimum chart where it is going down.
Griff, before your next post, answer my two questions.
I would not let you post until you do, but I tyhink you are here for entertainment, definitely not science.
Historically? You mean since 1979? When the winters here in North America became longer and colder? Such a pity the satellite data doesn’t go back to the 1930’s when summer temperatures were so high! Gee, I wonder how things looked back then? Or how about when the Vikings decided building colonies on Greenland was a hot, or at least warm, idea?
Seems like your historic time frame of reference might be a little short.
Remember the Last-First Arctic rower. They fell hook, line, and sinker for all of the predictions of melting ice. I still love this quote when they discovered the truth. It’s from the Vancouver Sun interview:
“I bolt upright with the banging noise, but don’t see a churning sea like I expect. “Holy shit,” I shout. “It’s ice!”
“In seconds, we are all on deck facing down a 100-foot ice floe that has wedged itself up against our bow. It’s being pushed hard from the storming wind and is moving directly over us. We try to release our anchor, but it’s stuck as this multi-ton piece of ice, some 30 to 40 feet thick, has positioned itself above it and is making it impossible to retrieve.”
“Pen Hadow, a British polar explorer, Erik de Jong, a Dutch sailor, and their crews sailed to within 600 miles of the North Pole, reaching a latitude of more than 80 degrees north”
Is that all? yawn-
1923
“In August the Norwegian Department of Commerce sent an ex-pedition to Spitzbergen and Bear island under the leadership of Dr. Adolf Hoel, professor of geology in
the University of Christiania, the object in view being to survey and chart areas productive of coal and
other minerals. The expedition sailed as far north as 81 deg. 29 min. N. latitude in ice free water”
http://trove.nla.gov.au/newspaper/article/168839462?searchTerm=arctic%20glaciers%20%20melting&searchLimits=
That is an excellent quote. I’m keeping that one.
“The expedition sailed as far north as 81 deg. 29 min. N. latitude in ice free water””
Still ice free at 81º23′ N.. WOW.. and that is without the aid of satellite ice charts etc .
There must have been a LOT LESS SEA ICE back then !!
Forecast weather for the upcoming week.
Today’s map.
High pressure builds across basin and moves into the eastern areas.
High pressure dominates eastern arctic, while lower pressure sets up over the western arctic.
With this pattern, we should see ice moving into the Laptev, and Siberian Seas from the north. Especially the Laptev, as the winds will be stronger.
OK, Tony, we’re sold. I know I am. We see fake news, fake data and failed predictions and projections everywhere we look. We see temperatures doing not a lot and AGW theory has more holes in it than a lump of Swiss cheese, but what next?
Seriously, how is this scam ever going to be put away?
Trump started strongly then exited Paris but has gone a little quiet (granted he has North Korea on his plate at present) and in the face of extreme non-cooperation he can’t fight this alone.
The UK body politic is still largely sold (especially on ‘renewables’) while the EU is off the scale stupid. Australia has just disgraced itself on energy policy based entirely on Saving the Planet. Meanwhile China, India and the rest milk the West for all they can while Russia is rolling around on the floor pointing and laughing.
What is the knock out blow? Where is the killer evidence from an insider that can unwind this scam? It’s so frustrating seeing your efforts come to so little in the way of official acknowledgement or policy change that this racket is nonsense on stilts. (plus Paul at notalotofpeopleknowthat plus WUWT, Jo Nova, GWPF, Dr Roy, NoTricksZone and many others, sometimes with slightly different takes on AGW theory but all highly sceptical)
The renewables racket continues apace and left-leaning MSM media STILL control the entire AGW narrative at the popular level, regardless of how brilliantly indy bloggers are performing. Where’s the kill shot, the KO punch, the Watergate Tapes or the blockbuster that simply can’t be denied?
PS and then there’s Ned’s paper. Would like to see that get a LOT more press coverage.
What next?
When we show cooling the AGW Kool aid drinkers will blame it on warming.
A few years back one of the climate scientists was asked if the Earth had 50 years of cooling, would this disprove the AGW theory. He replied that it would not in the slightest disprove the theory.
@Douglas Hoyt
Yes, that was a UK Met office scientists iirc. In short he was booting the entire farrago far enough down the track to see him to retirement. After that he clearly wasn’t bothered.
To answer my own question, it needs a new broom to sweep clean, and if Trump isn’t that broom and doesn’t sweep clean then I have no idea who will.
I thought Mrs May could’ve made changes after she succeeded Cameron but nope, she’s as bats as the rest of them!
A comment from one of the AGW CO2 haters.
“this cold was caused by the anthropogenic global warming and could be the starting of a new glacial age.”
Say what ?? !!
What’s the “cost” in CO2 for this exploration nonsense. They’ve got some big old ship tagging along to give them respite from “harsh conditions.” So they’re not bivvying in the kayaks, right.
Not that I blame them. Whatever else you say about these boutique recreational activities they can be damned uncomfortable and I respect the effort. Fact is you’re probably going to need some kind of climate berzerker trustifarian to fund your activities. Yeah, get that.
But don’t go out there w a hotel following you around and expect to be taken seriously telling us “oh the poor polar bears. Can’t adapt to climbing for coconuts.” Many have paid the ultimate price for messing about in boats in the freezing cold. These guys, not so much.
Since it is relevant to this post, I will once again make some observation on Arctic temperatures.
There has been no global warming in the vicinity of Greenland for nigh on 80 years.
Both Greenland and Iceland show the 1940s as their warmest period during the time of the thermometer record (when RAW temperature data is used).
Hadcrut area weighted 70deg to 90 degN shows that 2016 has a 27 month smoothing anomaly figure of + 1degC and 1936 and 1944 had a similar + 1 degC anomaly.
If one takes out the smoothing, Hadcrut shows 1936 with a + 7degC anomaly and 2015 with a + 4 degC anomaly (2016 being cooler than 2015). See;
http://notrickszone.com/wp-content/uploads/2017/04/Arctic-Temperatures-1920-2017-HadCRUT4.jpg
If one looks at the 24 year period between 1922 and 1946, and compare this to the 24 year period between 1992 and 2016, and note the number of years where there has been around a + 4degC anomaly, one notes that during the period 1922 to 1946 there are 12 years with this or greater anomaly (ie., half the period) whereas during the period 1992 to 2016 there are only 6 such years.
It is clear that it was generally considerably warmer in the Arctic during the period 1922 to 1946 than it is during the recent period 1992 to 2016. Not only are there more + 4 degC anomalies during the earlier period, the peak anomalies are higher.
It is quite clear from this that if there is any material ice loss in the Arctic it is not due to global warming, simply because there has been no material warming in the Arctic region over the course of the past 95 years.
One can see from the Hadcrut record that there is absolutely no correlation between temperatures and CO2, and further during the period when manmade emissions started escalating, late 1940s on wards ,generally temperatures in the Arctic have been cooler than they were prior to the date of escalation, ie., during the period prior to the late 1940s.
Griff wants to know how can the sea ice have declined since 1979 is if wasn’t any warmer?
The answer to this question is Simple.
The decline in sea ice is not due to warmer air temps, but rather due to variations in warm currents, AMO and wind/storminess.
Further, of course, on a historic basis there has not been the decline in sea ice that Griff imagines that there has been.
There is more sea ice now than there was in the 1920s. That is why the recent Pen Hadow sailing expedition came to a freezing halt and could go no further than “80 degrees 10 minutes North, 148 degrees 51 minutes West, reached at 22:04:12 (Alaskan Time, GMT-9hours) on 29 August 2017 by yachts, Bagheera and Snow Dragon II.” Likewise, it is why the earlier British rowing expedition got blocked by ice on 10th August 2017 just off the North West coast of Svalbard at about 79°55’50” N.
Whereas, in 1922 the Norwegian Department of Commerce sent an expedition that reached 81°29’ North. This is more than 1 deg further North, and the expedition was not blocked by ice. It still reported ice free waters.
The contemporaneous newspaper report is set out:
https://biasedbbc.org/wp-content/uploads/2017/09/ice2.jpg
richard at September 4, 2017 at 5:15 pm also makes a similar point.
The fact is that there has been quite a lot of multidecadal variation in temperatures, but overall there has been no warming, and today the sea ice is not substantially less than it was in the 1920s. This is also borne out by the Vinnikov et al 1980 paper (Vinnikov is one of the three lead authors of the first IPCC report Chapter 7 dealing with climate variability).
“Winds from Siberia reduce Arctic sea ice cover, Norwegian researchers find”
https://www.sciencedaily.com/releases/2010/04/100427111449.htm
These are the kind of “scientists” Griff follows. Note that Steve Ferguson also works with David Barber who said the Arctic would be ice free in 2008.
“Climate Change on fast-forward in Arctic, U of M scientist warns”, in the Winnipeg Free Press on Dec 7
Full article in:
https://www.winnipegfreepress.com/local/climate-change-on-fast-forward-in-arctic-u-of-m-scientist-warns-405091456.html
Part of article:
A near-catastrophic plunge in the population of ringed seals in Hudson Bay is being blamed on melting sea ice caused by global warming, says a study led by a Manitoba researcher.
The population has been diminished by 75 per cent since aerial surveys started 20 years ago, according to data that will be presented to the ArcticNet conference of scientists in Winnipeg this week.
Lead researcher Steve Ferguson, a scientist with Fisheries and Oceans Canada and the University of Manitoba, said global warming is causing sea ice to disappear earlier in spring and form later in the fall, and there is less of it in Hudson Bay.
Ringed seals feast on smaller fish beneath the ice. The food around ice has lots of fat, important in the Arctic where animals need to build up body mass to survive the extreme conditions. Seals also depend on sea ice for molting in late spring when they change their coats.
Bearded seals, which forage under ice for food such as clams, are also likely to be negatively affected, he said.
And in turn, the polar bear population will suffer because seals are the main component of their winter diet. The problem is compounded, as less sea ice means the bears have less area to hunt.
Hudson Bay could experience its first ice-free winter within five to 10 years, Ferguson said
“I don’t think polar bears and seals will be able to adapt. I think they’ll just die out in places like Hudson Bay. There’s little to stop the trend in loss of sea ice, even if we stop producing greenhouse gasses,” he said.
***A near-catastrophic plunge in the population of ringed seals in Hudson Bay is being blamed on melting sea ice caused by global warming, says a study led by a Manitoba researcher.
The population has been diminished by 75 per cent since aerial surveys started 20 years ago, according to data that will be presented to the ArcticNet conference of scientists in Winnipeg this week.***
What the article does not say is how they do the surveys. They do strip flights counting the seals below. Then they expand the fraction covered extrapolating to cover a larger area to get a total. Some years later they cover the same area to fins there are less seals. What they do not account for is that the seals have moved to where there is more ice. The “scientists” now tell us the seals have decreased by 75 percent and the polar bears are in trouble. the polar bears have also moved to where the seals are and we know that the bears HAVE NOT DECREASED.
Its nature purely cyclical our leaders are in it for the money this will be the biggest farce in history i worked in the arctic for 10 years its crime to scare people. We may need to chane our way of doind business but we are getting it shoved down our throats . We will have another ice age and now were in a warming cycle. ocean currents control our weather. At any given time we have hundreds of active volcanos spewing millons of tons of green house gases in to our atmosphere. Scientists are global economy killers its not that hard to figure out we have done 3000 meter core samples in the arctic and Antarctic. We must take a stand on billions of dollars wasted on a huge lie.
Gee, that Arctic Mission to the North Pole is charging back to Alaska. So now we will never know if there is ice at the pole.
I hear it’s all gone. That’s why they didn’t bother.
What is really funny is that stupid trolls like Jim H. was saying over and over it was a SCIENTIFIC mission,but golly as soon as Pen and his band of clowns realize the Pole is deeply iced in,they quickly turn around heading for Nome.
They quickly dropped the Science mission for the warm fireplace in Alaska.
LOL
This is an interesting article from 1983. It details a lot of findings concerning the little ice age and the MWP. Such references are still useful today to show temperatures were higher during the MWP than now. There is much evidence indicating great shifts in temperature in the North Atlantic, areas including Iceland, Greenland, Canada, and so forth. The evidence indicates times both colder and warmer than seen in the modern satellite era.
http://www.grisda.org/origins/10051.htm
Then there is this. Contradicts the cult of global warming every way from Sunday.
http://www.ncpa.org/pub/st279
Is this wrong then?
(attached screenshot)
– Just interested – I know next to nothing about climate science.
Sorry – that is Artic see ice minimum – 1979 – Now.
It shows the same thing. No change over the past 10 years.
Jules, Yes the Arctic sea ice has declined since 1979.
But the late 1970’s was actually an extreme HIGH level of Arctic sea ice.
Icelandic sea ice record shows that late 1970’s was actually up there with the levels of the Little Ice Age
https://s19.postimg.org/bkgbf2prn/Icelandic_sea_ice_index_2.png
And studies using biodata from sediments around the Arctic show that:
1. Levels through the first 7000 or years of the Holocene were a LOT lower than now, often being effectively ice-free in summer
2. About 3000 years ago sea ice started to increase. Through the Medieval warm period the levels were still considerably less than current
3. Sea ice grew to near perennial levels during the LIA (coldest period in 10,000 years)
4. Current levels have dropped since then, but not down to the levels of the MWP.
So you see, if taken in a longer term perspective, the current level is actually HIGHER than it has been for some 90-95% of the last 10,000 years.
Its only looking at the level as it has dropped down from extreme high levels that any “scare” can be manufactured.
How was sea ice extent measured prior to the modern era – or how are able to say for sure exactly what the extent was?
……load Homer Simpson voice…….Stupid ice!!